语雀新画板,seeconf,设计故事

语雀新画板

话不多说，直接进入我今天分享的主题，我今天分享的主题教育就是新画板。其实关键字就一个字新。然后什么是新呢？我将从上面五个方面去讲，分别是新功能、新用法、新问题、新思路、新方法。

新功能，新⽤法

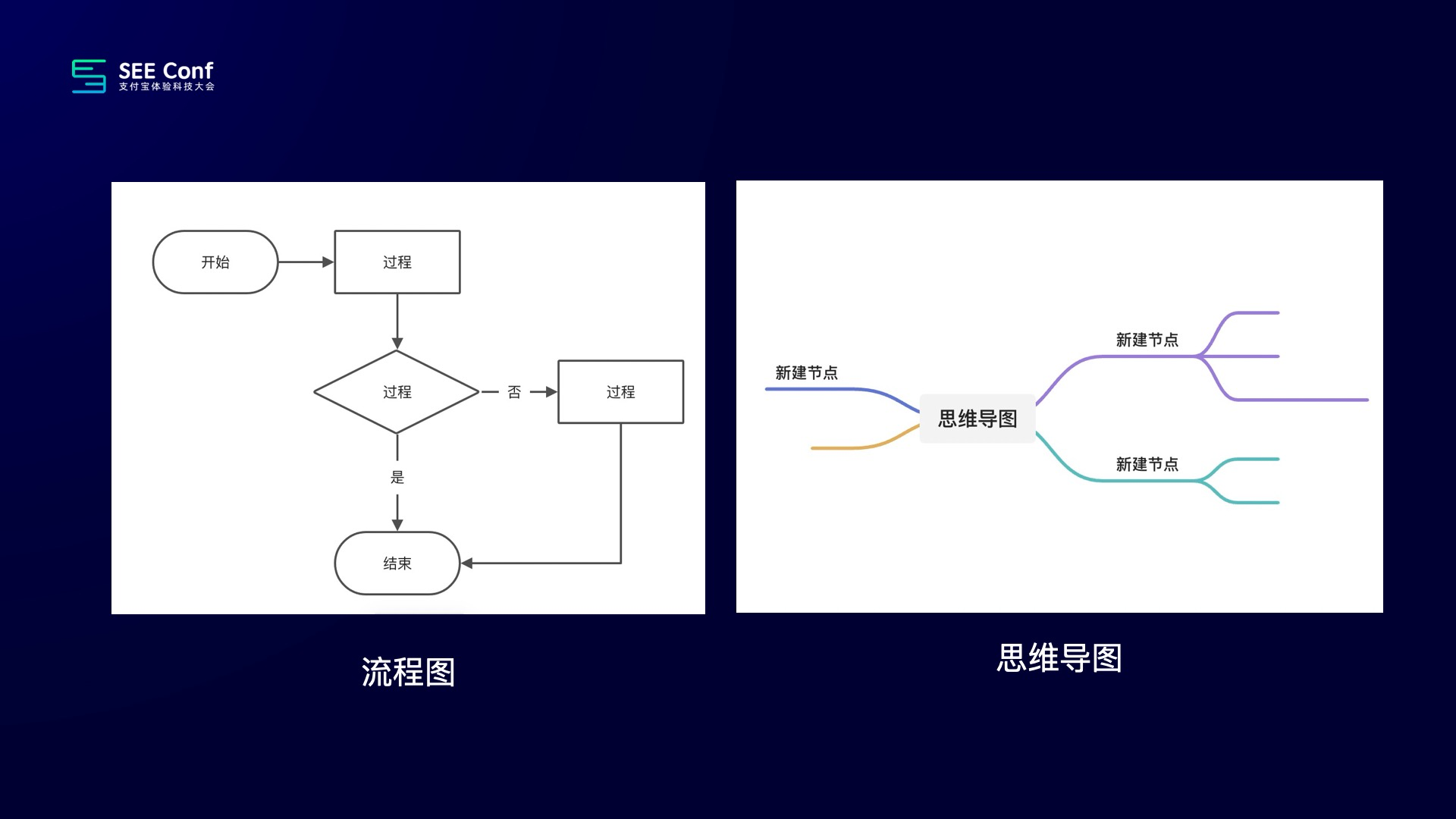
其实语雀画板这个项目还是蛮新的，因为最近今年才刚上的。但是如果加上语雀画板的前身，思维导图、流程图其实已经上了很久了，算上这两个，整个画板项目其实已经做了两年多，快三年了。

今年画板产品层面最大的一个改变，是这两张图能在同一张画布上去画。做完这个功能的时候，就理所应当的出现了很多我们意料之中的场景。比如下面这幅图就融合了思维导图和流程图。

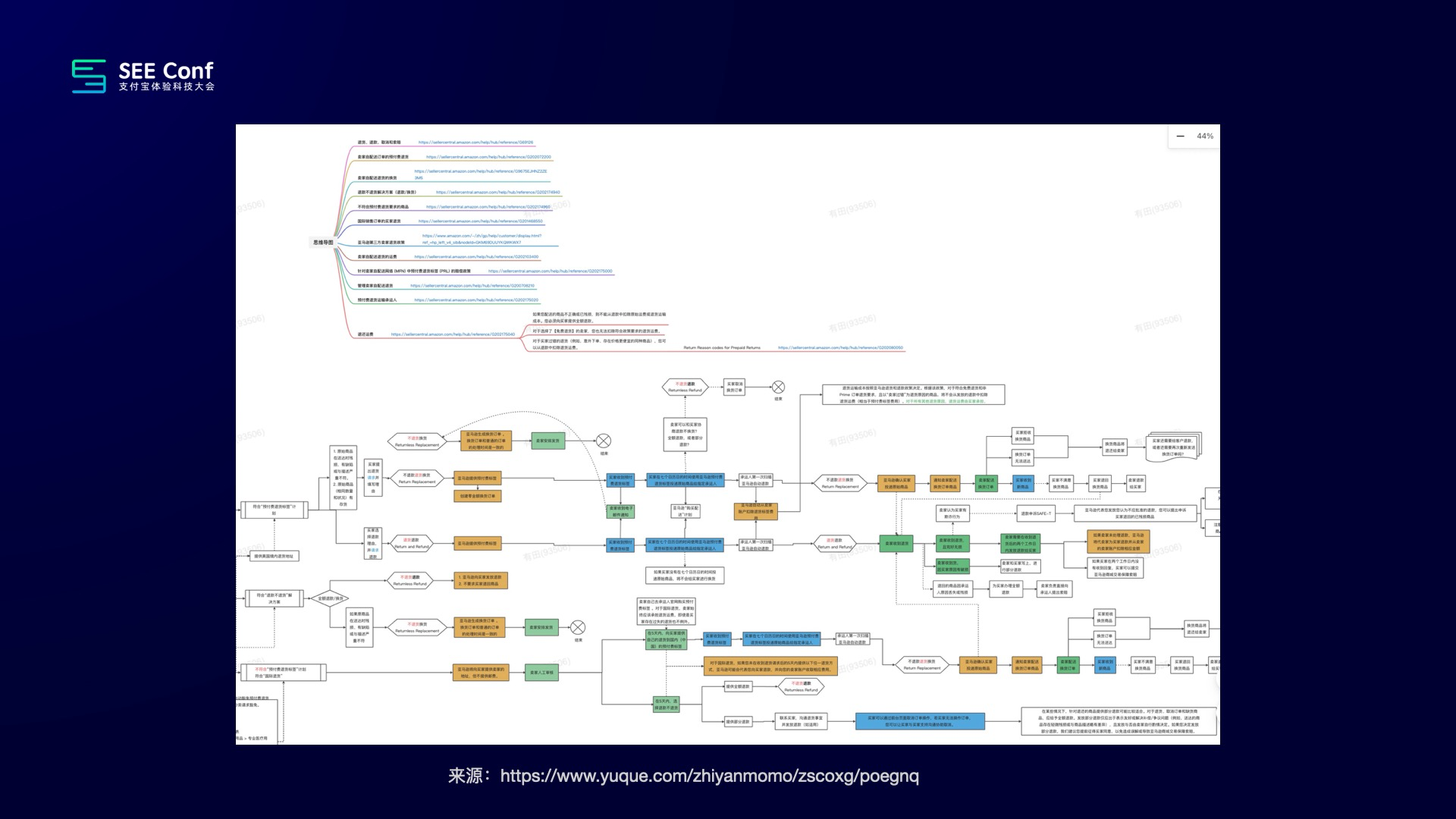
但除了意料之中的场景，也出现了许多我们意料之外的场景。比如说这幅图，这幅图就比较有意思了，就是你乍眼一看，不知道里头到底是思维导图还是流程图。但其实这个里头也是既有思维导图，又有流程图。他用思维导图去做了一个结构，然后用流程图的那个四边形去画了菱形的样式。

此处为语雀视频卡片，点击链接查看：Jan-05-2022 17-01-54.mp4

过去的一年，除了把两张图融合以外，我们还做了很多基础功能的升级。比如，我们现在是可以手动的去调线的路由。

然后做完这个功能以后，也理所应当的出现很多我们意料之中的用法。

同时也出现了一些我们意料之外的用法。

这两个例子，总结起来就是一句话，就是：

吹完这个牛逼的时候，本来想继续往下吹的时候，这时候就有个人跳出来说：“等一下”。说到这里，大家可能不知道像 SEE Conf 这种这么高质量的会议，每个议题都是有试讲环节的。之前在我试讲的时候，我的评委就说了这么一句话：

好，既然屏幕前的你们都是产研界的专业人士，那我知道后面我应该讲什么了。

接下来进入我们今天分享的主要环节，就是语雀画板在过去几年中碰到的新问题、新思路以及解决问题的新方法。

新问题，新思路，新⽅法

这部分，我将通过三个故事引出。第一个故事是关于一个树的故事。话说在很久很久以前，就有一个树形的数据。

这一串树形数据机器很容易能读懂，但人却很难。所以最早就有一帮程序员跳出来说，我要把这个数据可视化一下。

首先第一个登场的是一个叫 Knuth 的大神（他的中文名叫高德纳，计算机领域可能都认识他，因为他真的是宗师泰斗级的人物）。他提出了以下几个原则：

然后大师大手一挥，写了九行代码，写了一个布局算法出来。

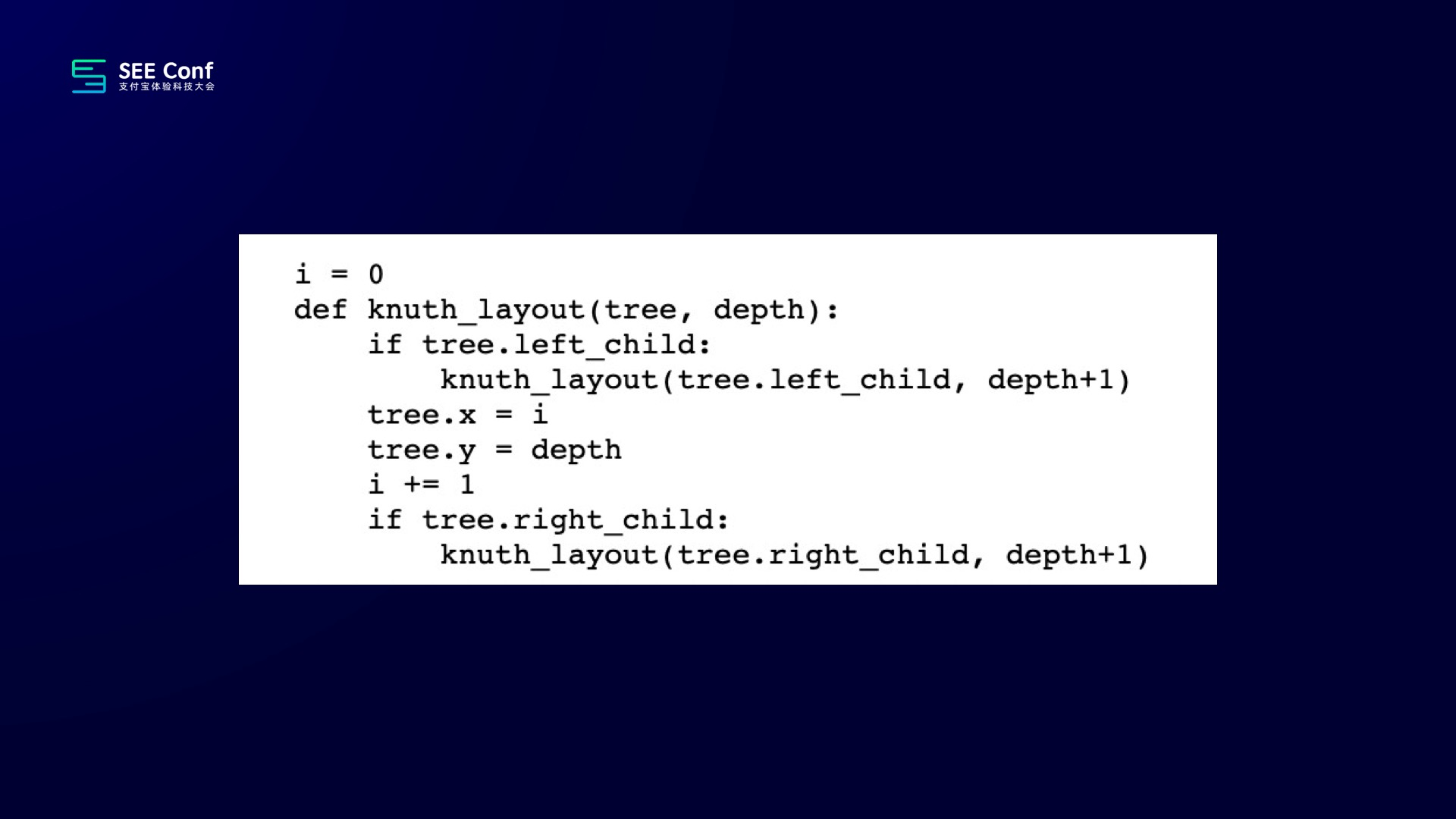
开始他想象中的是左边的这个效果，但其实他那个算法跑完以后，实际效果是右边那样子的。

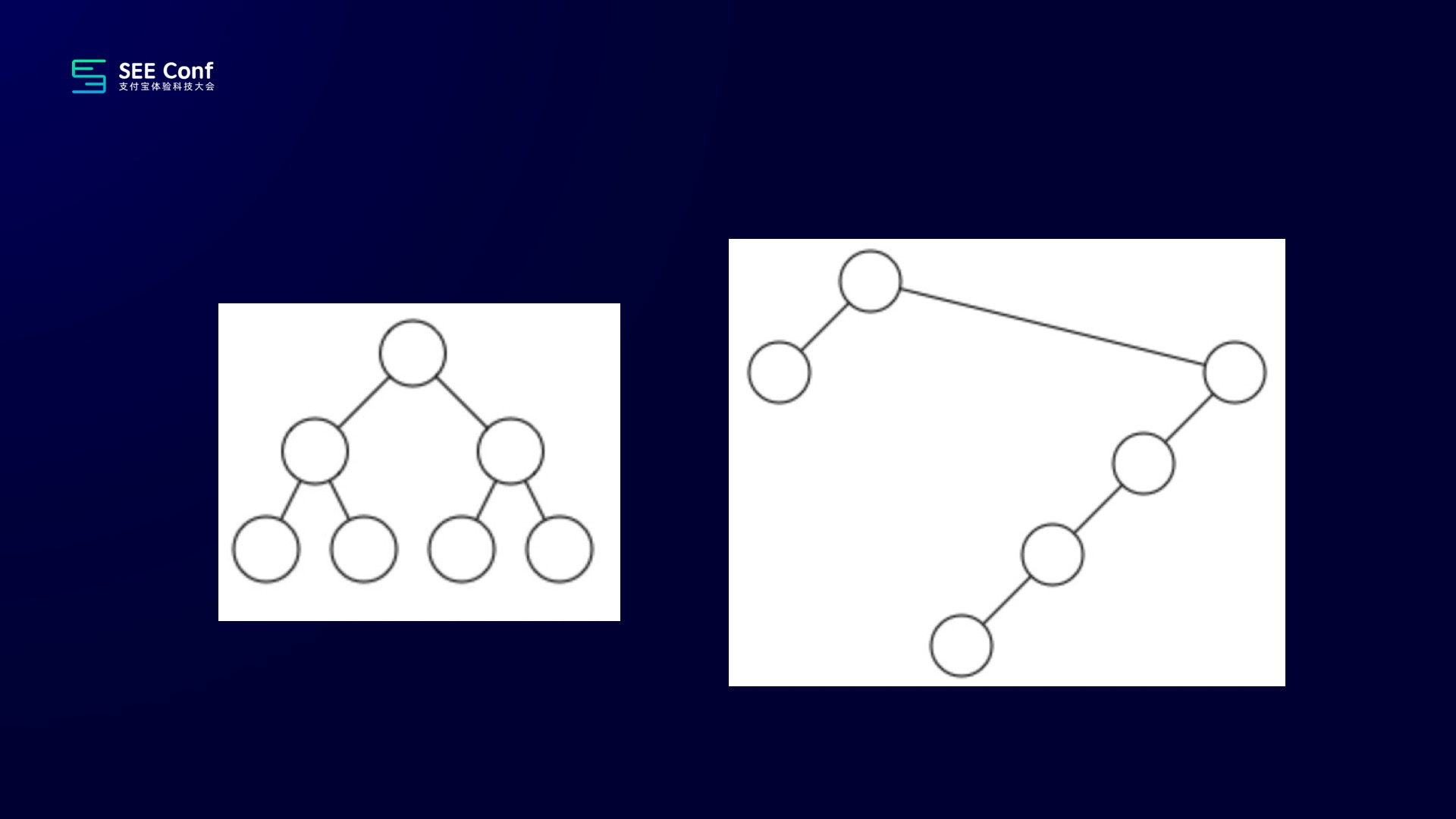
虽说右边的效果不尽如人意，但也没有违反他在做这个算法前定的那两个原则。于是乎大师也就满意的结束了这项工作。

但过了几年，又出来两个人。一个人叫 Charles Wetherell，一个叫 Alfred Shannon 。他们就觉得刚才那个效果不够好，于是他们又提出了两个原则：

做完以后，虽然效果仍然不够好，但也同样满足了，他们最开始提的原则。

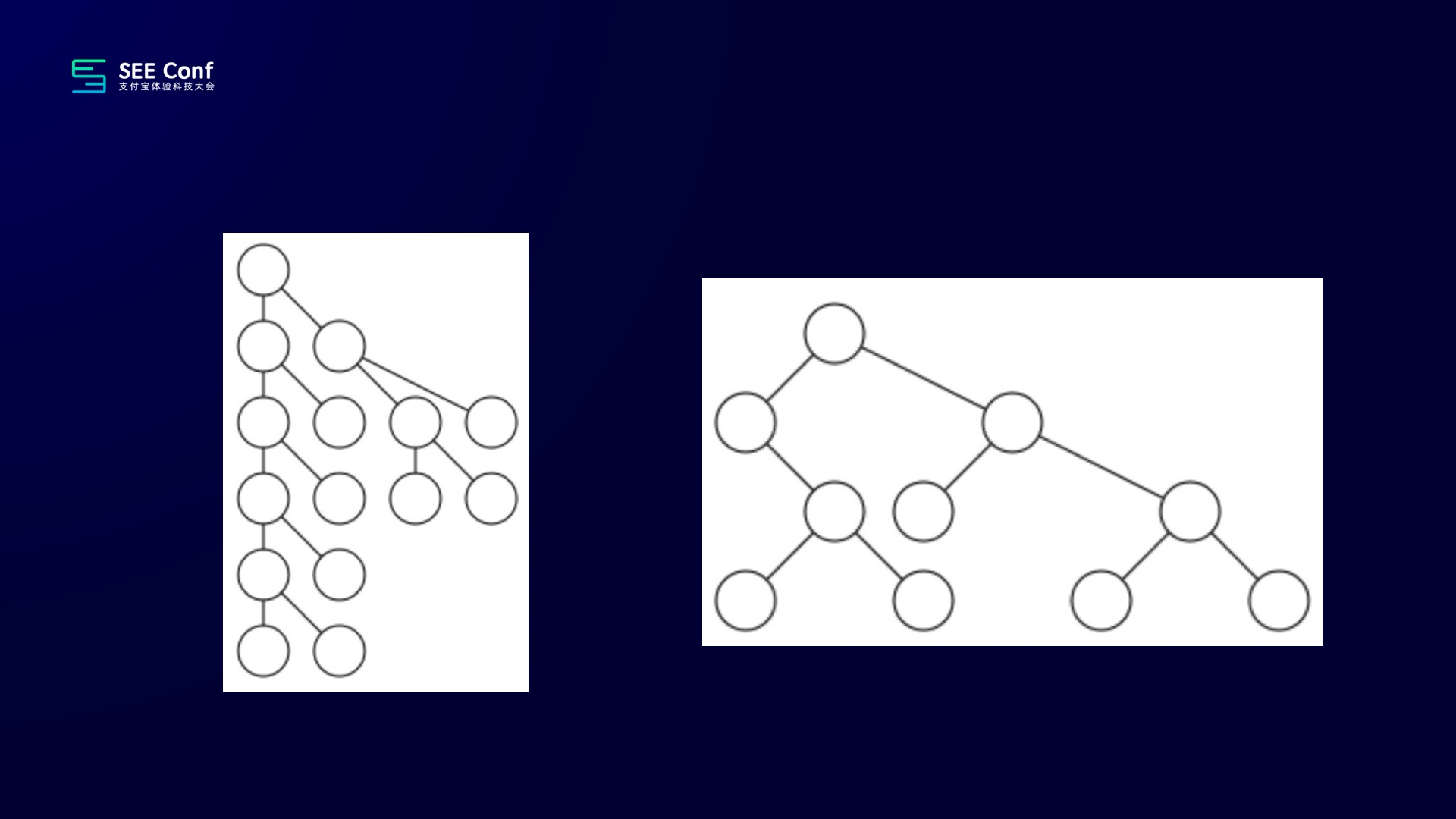
紧接着后面又出来两个人，他们又在前人的基础上增加了两个原则：

最终这两人，得到了比较好的效果。并总结出了，我们现在比较常用的紧凑树的布局算法。

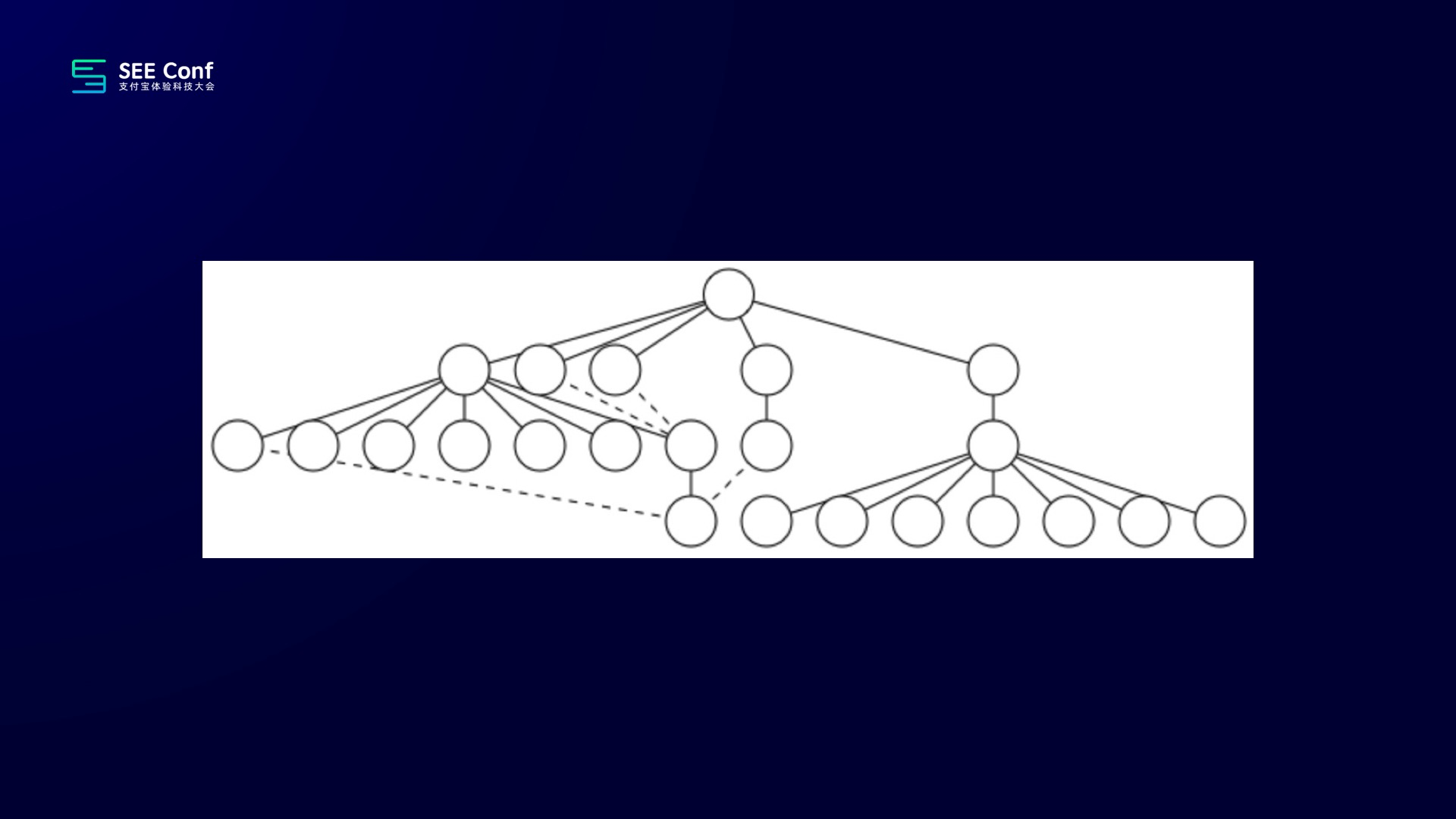
刚刚这个故事来自于这篇文章，回顾一下，虽然说就那么简短的几个片段，但是这个过程其实经历了整整十年。

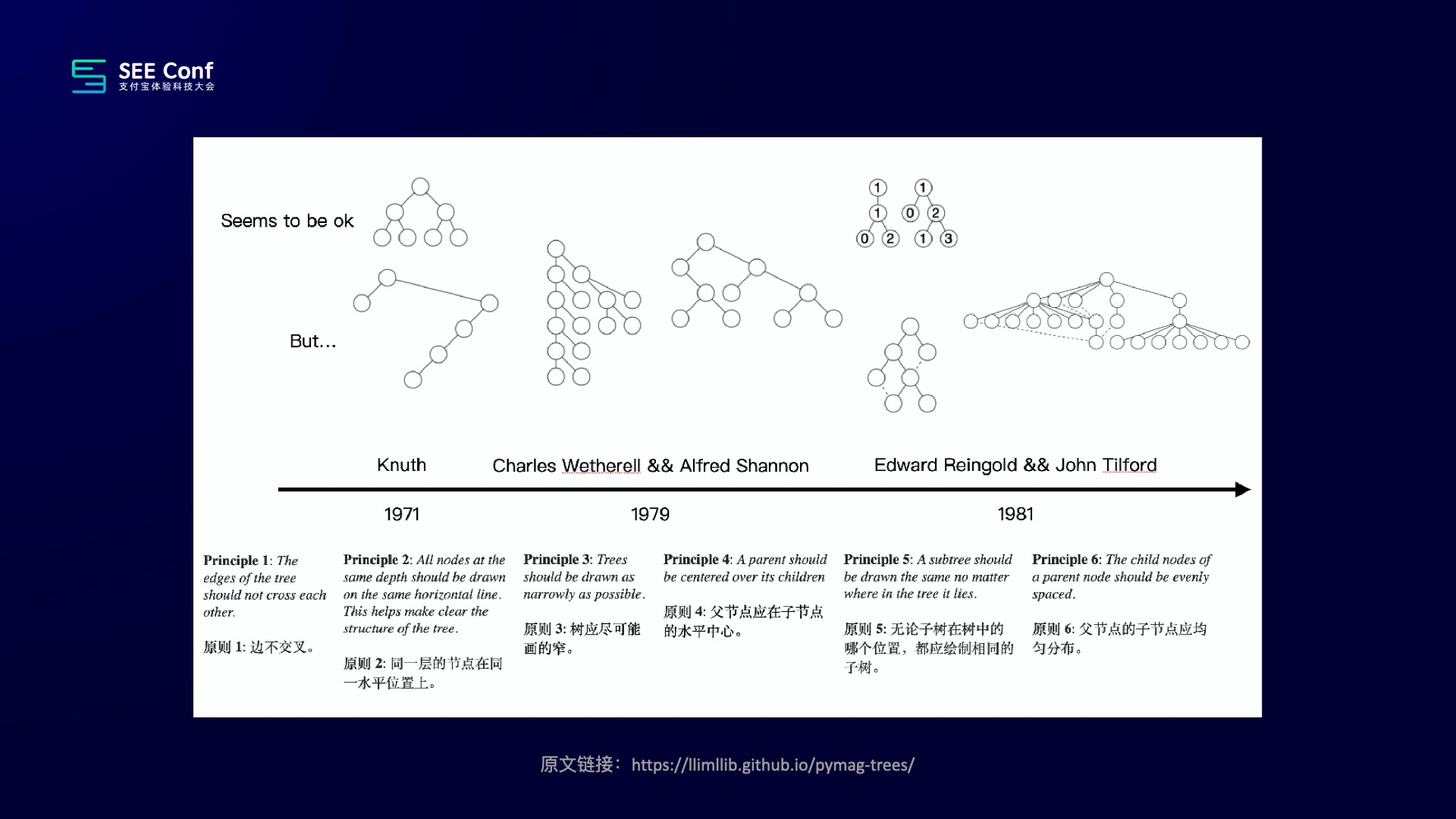
老实说，当我看到这篇文章的时候，我是比较惊讶的，好像一个很常用的一个算法，竟然是通过几代人的摸索才最终把它完成的。但不管怎么样，有了这个算法以后，我们刚才最开始的树形数据就可以被很清晰的可视化出来了：

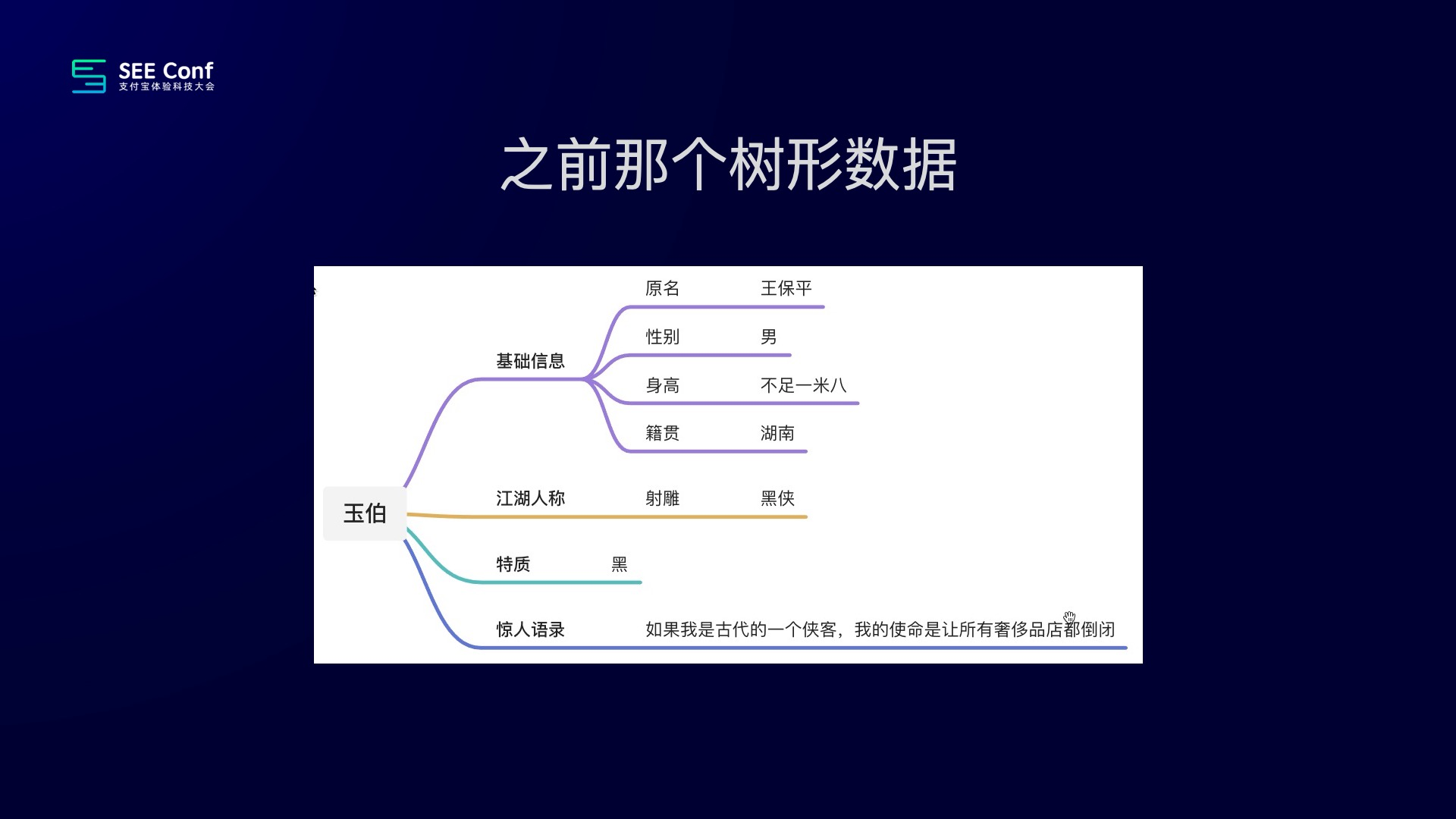
看到这，可能会有人感慨：还好现在既不是古代，玉伯也不是一个侠客

为什么要讲刚才那个故事呢？其实还是因为我们要做思维导图时，思维导图的算法的核心就是受刚才那篇文章的启示，最终才做出来的。但是除了那个算法本身以外，其实刚才那篇文章对我个人来讲的话，最大的一个影响是：我知道了他怎么去把一个事情做好的一个整个流程（我个人认为，对我现在工作影响最大的一个东西），我将其总结为：六块砖（抛砖引玉）

第二个故事，关于一根折线的路由。

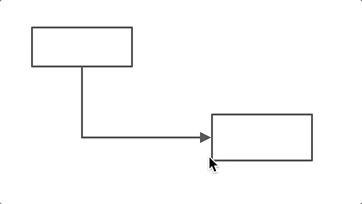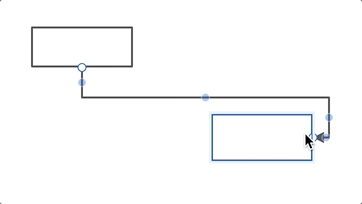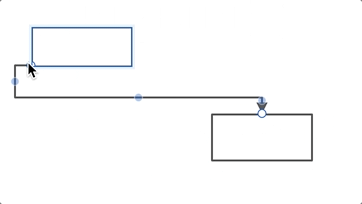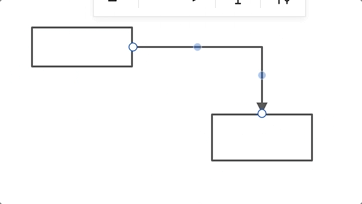
在做这件事情的时候，当时的情况就比之前做思维导图布局时候要差。因为我们没有找到现成的算法，现成的解决方案。但没关系，我们有六块砖。所以我们就用六块砖的思路去解这个折线的那个事情。

首先，我们就是通过调研竞品，枚举场景，发现问题。

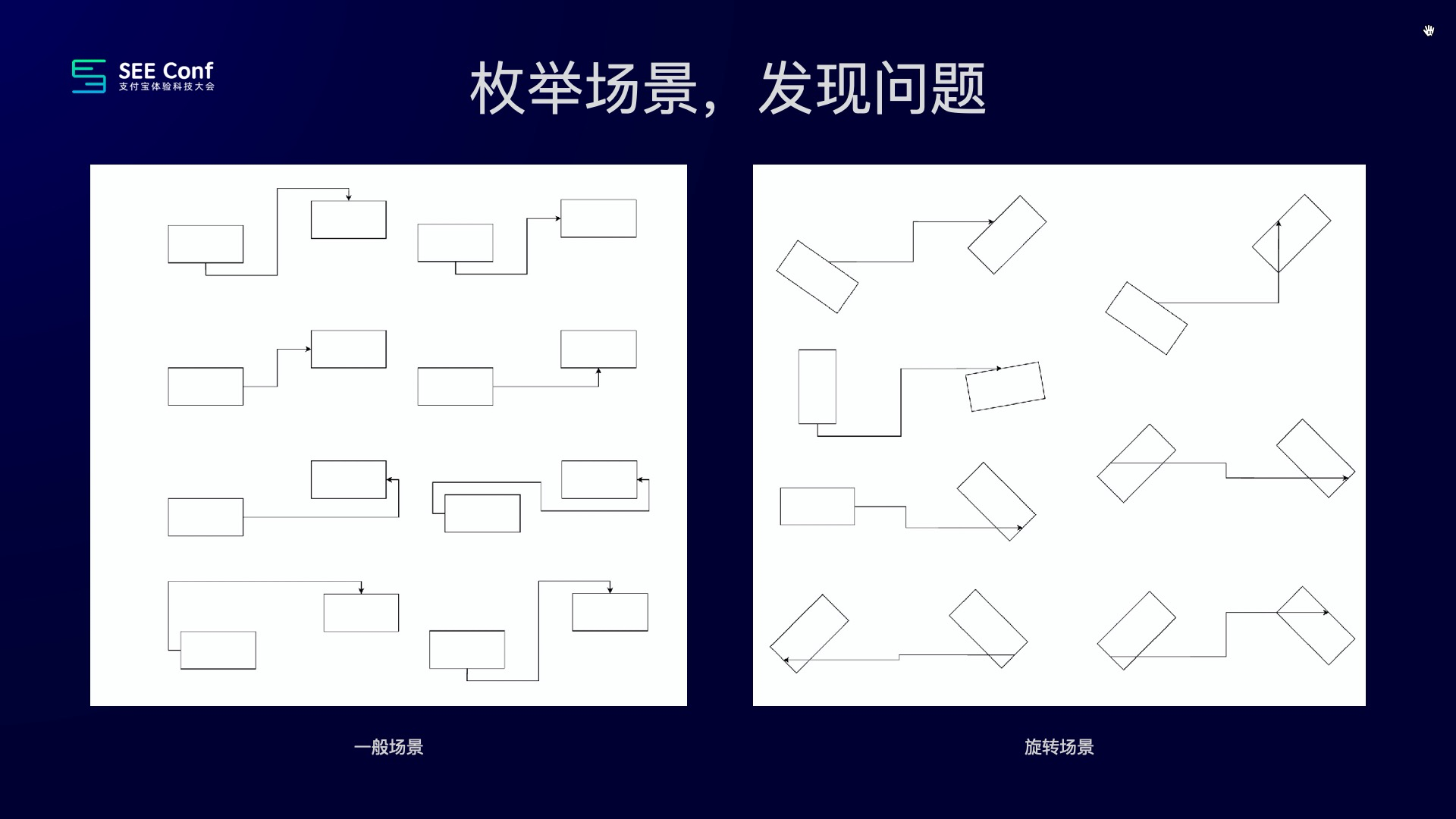
通过，调研、分析，我们抽象了以下六个原则：

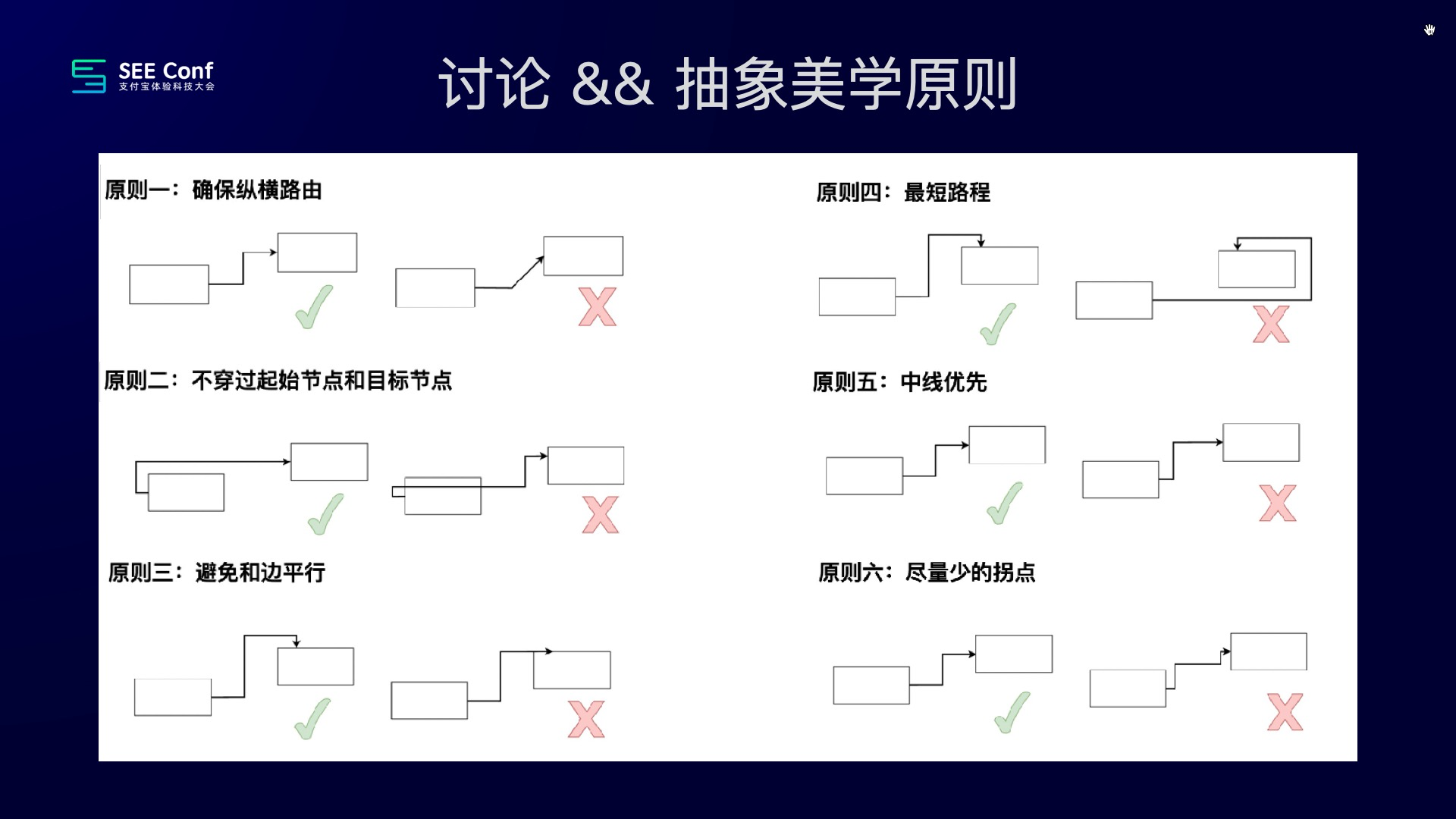
基于这那个抽象的原则，其实就可以进入技术环节了。但技术方案讨论起来过于详细，可能会非常耗时，所以这里肯定是没有时间跟大家展开的。但是我们还是把我们这个算法的核心的一些东西跟大家介绍一下。就是我们把那个折线的问题给收敛到图的寻径问题，并且借鉴了 A* 的思想，再把刚才的美学原则给体现在到 A* 算法的评估函数里。

最终，我们整个方案最终跑出来的效果还是比较好的。左边是一般场景下竞品的效果，右边语雀画板的效果，大家可以看到两者表现是基本一致的，如下图所示：

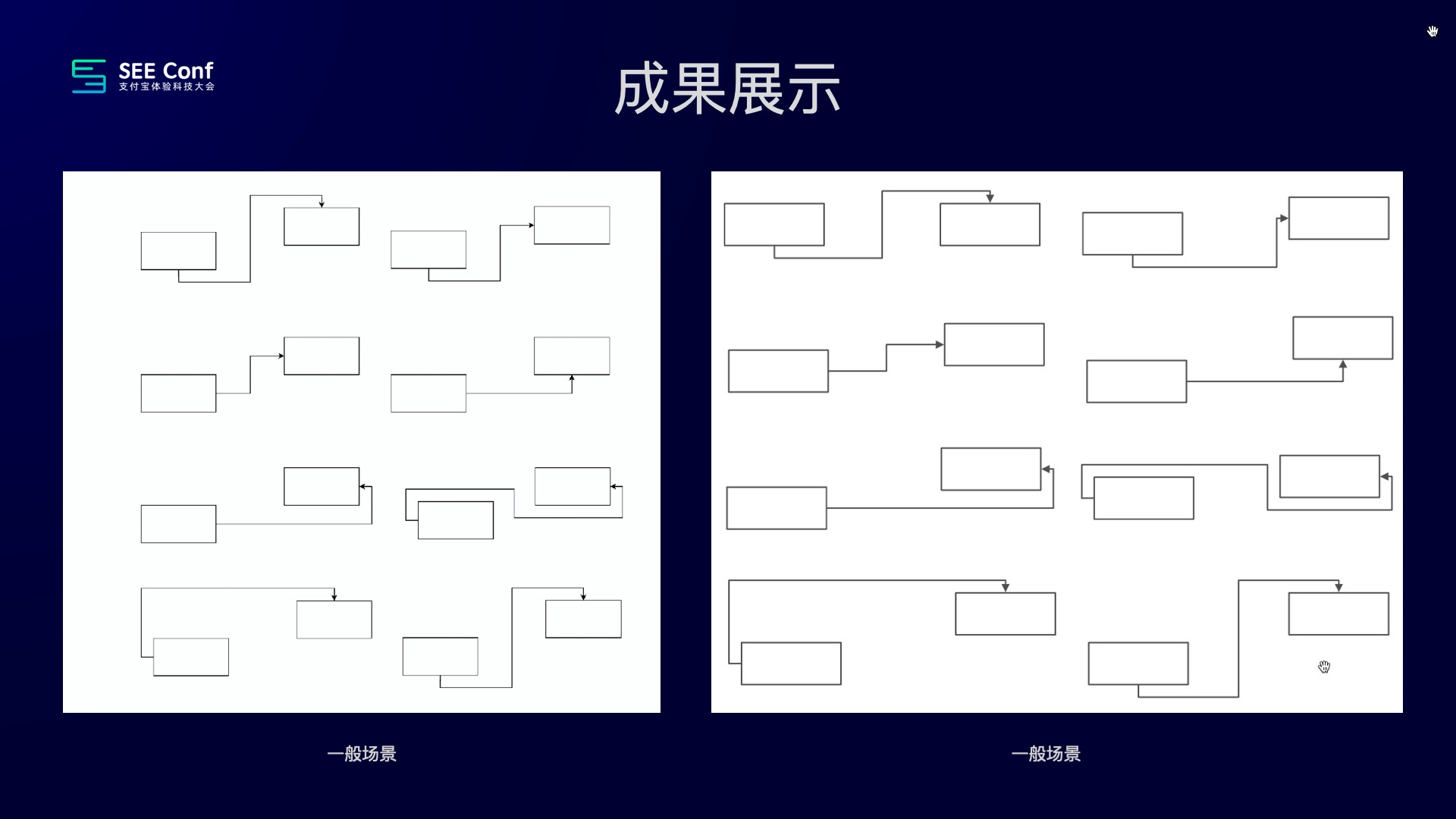
但对于节点发生旋转的场景，就不大一样，同样的左边是竞品的表现，右边是语雀画板的表现。

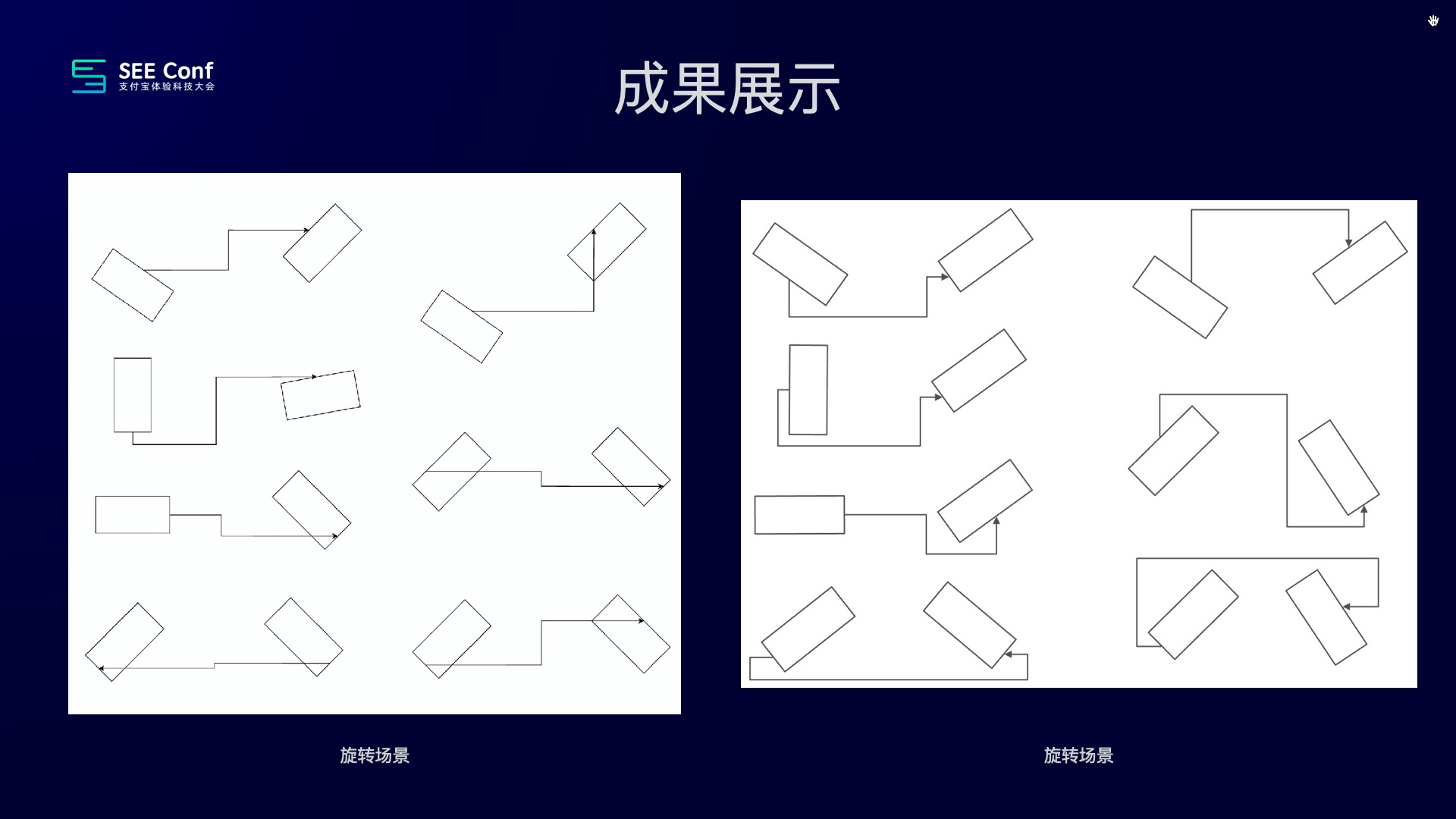
至于为什么表现是这样，有点意料之外，因为算法是抽象的逻辑，没跑出来，我们无法想象所有的结果，也有点意料之中，因为我们的算法设计要遵循上述原则二：不穿节点。所以如果基于我们最初提出的美学，那么我们认为在这块效果，我们是优于竞品的（这大概、也许、可能算一个小小的创新吧 ^_^）。

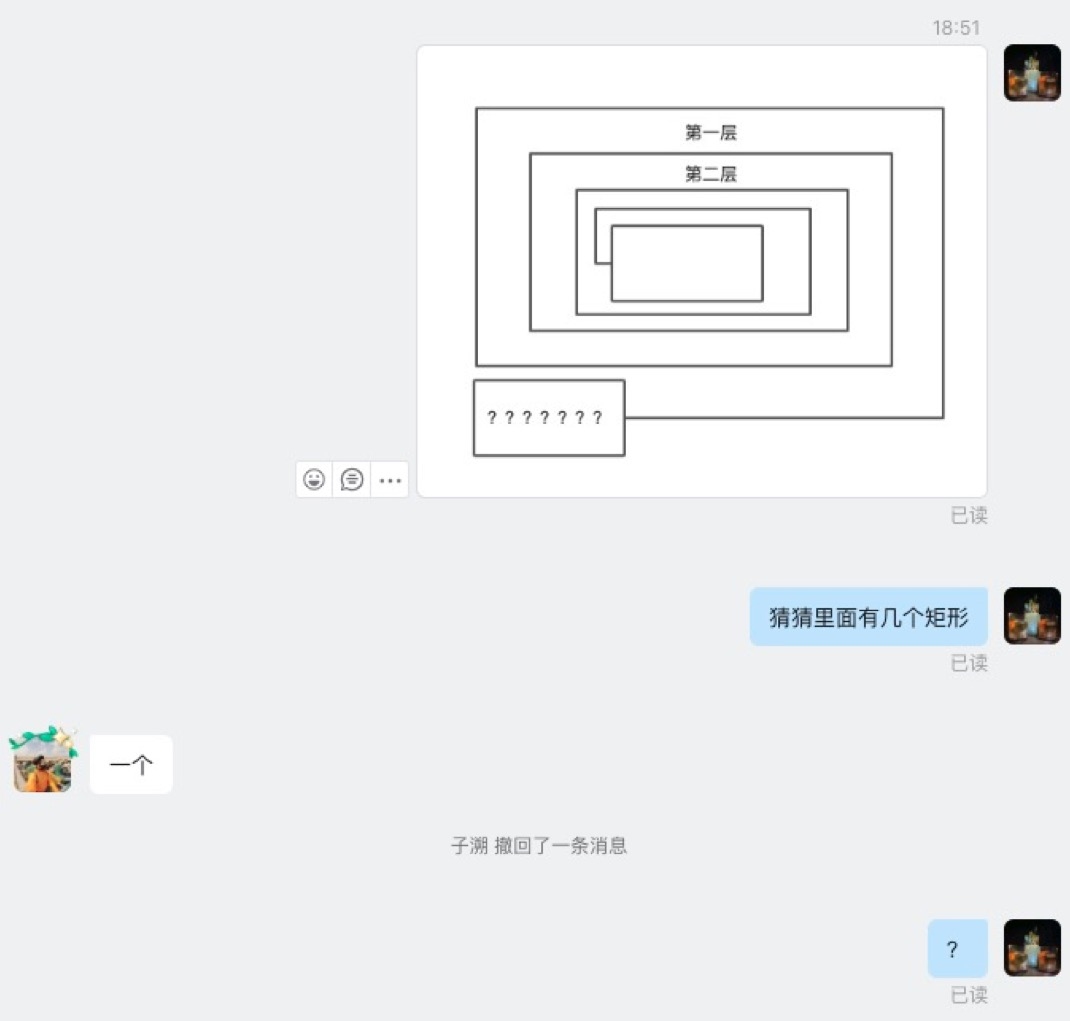
好，这个故事讲完了，还有最后一个故事是关于思维导图的子图结构嵌套（下文简称：子图嵌套）。

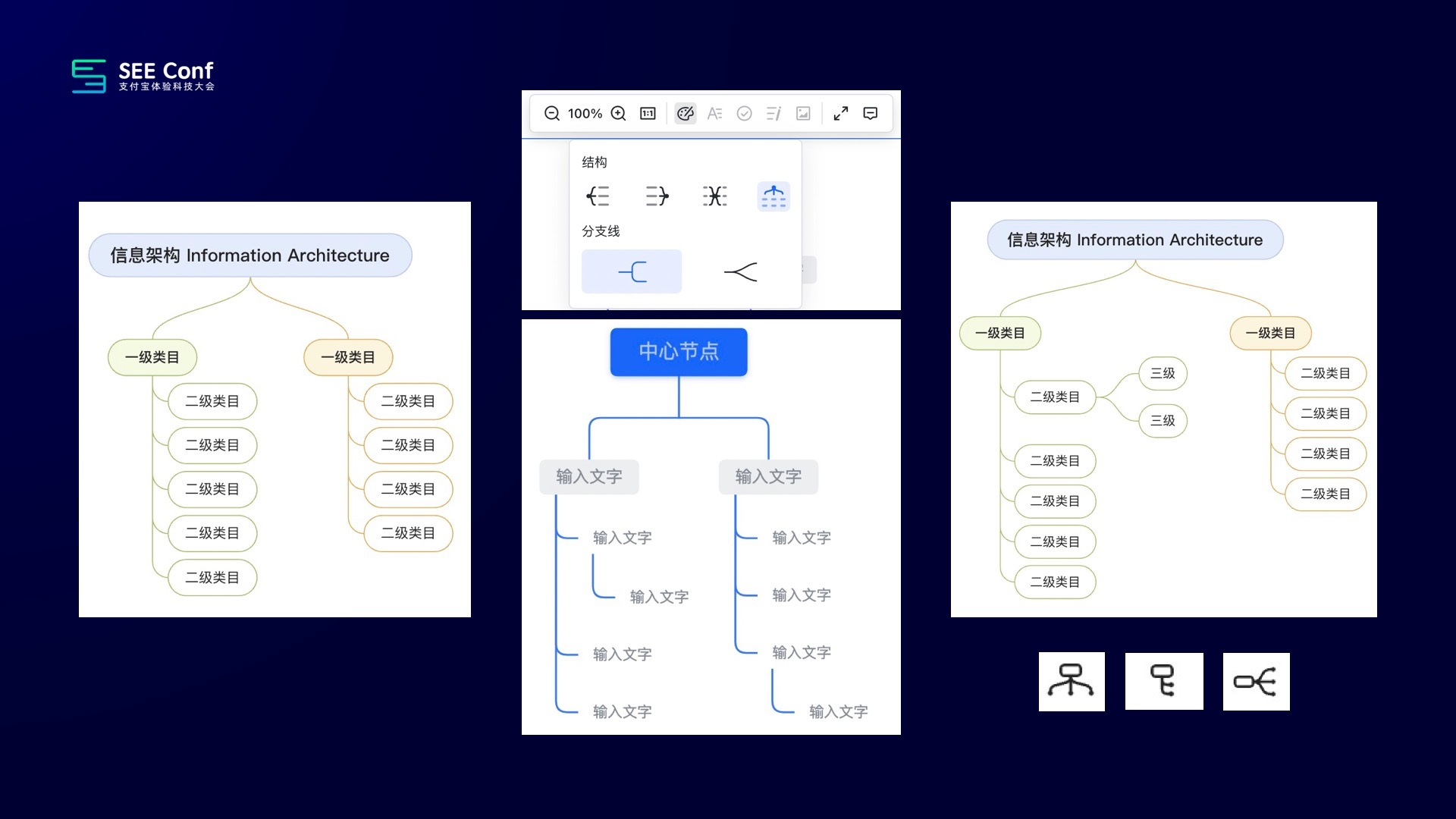
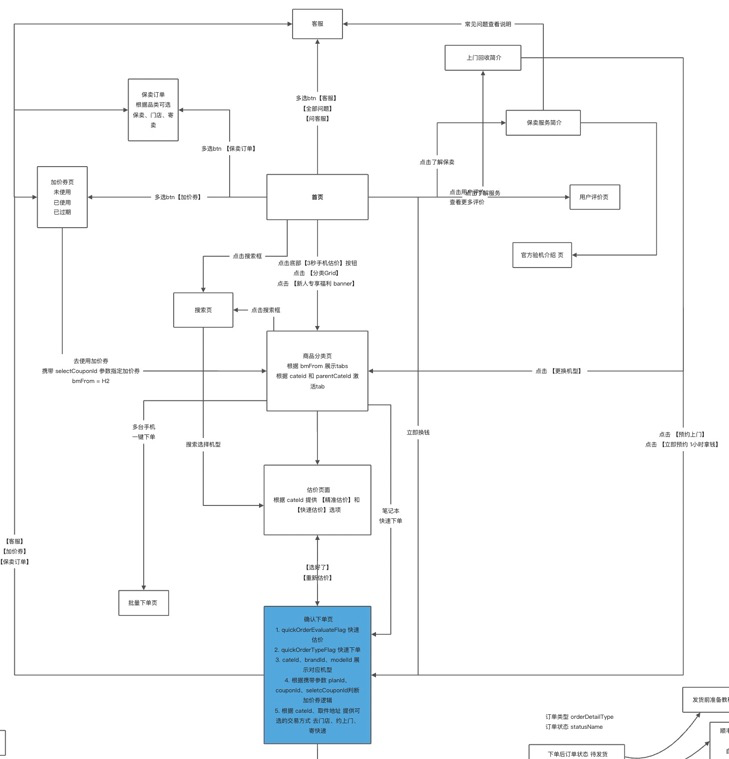
故事的开头是这样的，突然有一天产品经理说我要画这个图（上图：左一），然后我一看，这个图不难，很简单，我们完全可以参考某钉或某书的做法（上图：中间），就给一个固定的一个结构，写一个固定的布局算法就可以搞定了。但紧接着产品经理说，我还要画这种图（上图：右一）。这个时候作为一个从业多年的前端程序员，这个职业的敏感性就上来了。产品的想要的肯定还有图四、图五、图六……图 N。如果用写死的布局算法，那我不是要写一堆的算法去支持？所以这里肯定不能用一个针对每个case都去写一个布局算法的方式。于是乎，我们借鉴了思维导图界业界的龙头老大，某 Mind 的做法，就是让图的结构可以相互组合，相互嵌套。

做这个事情的时候，当时的条件就更差了，因为我们不仅没有现成的技术方案，甚至竞品做的也不够好（如下图所示），所以相对来说，在做这件事情时，也没有成熟的产品方案。

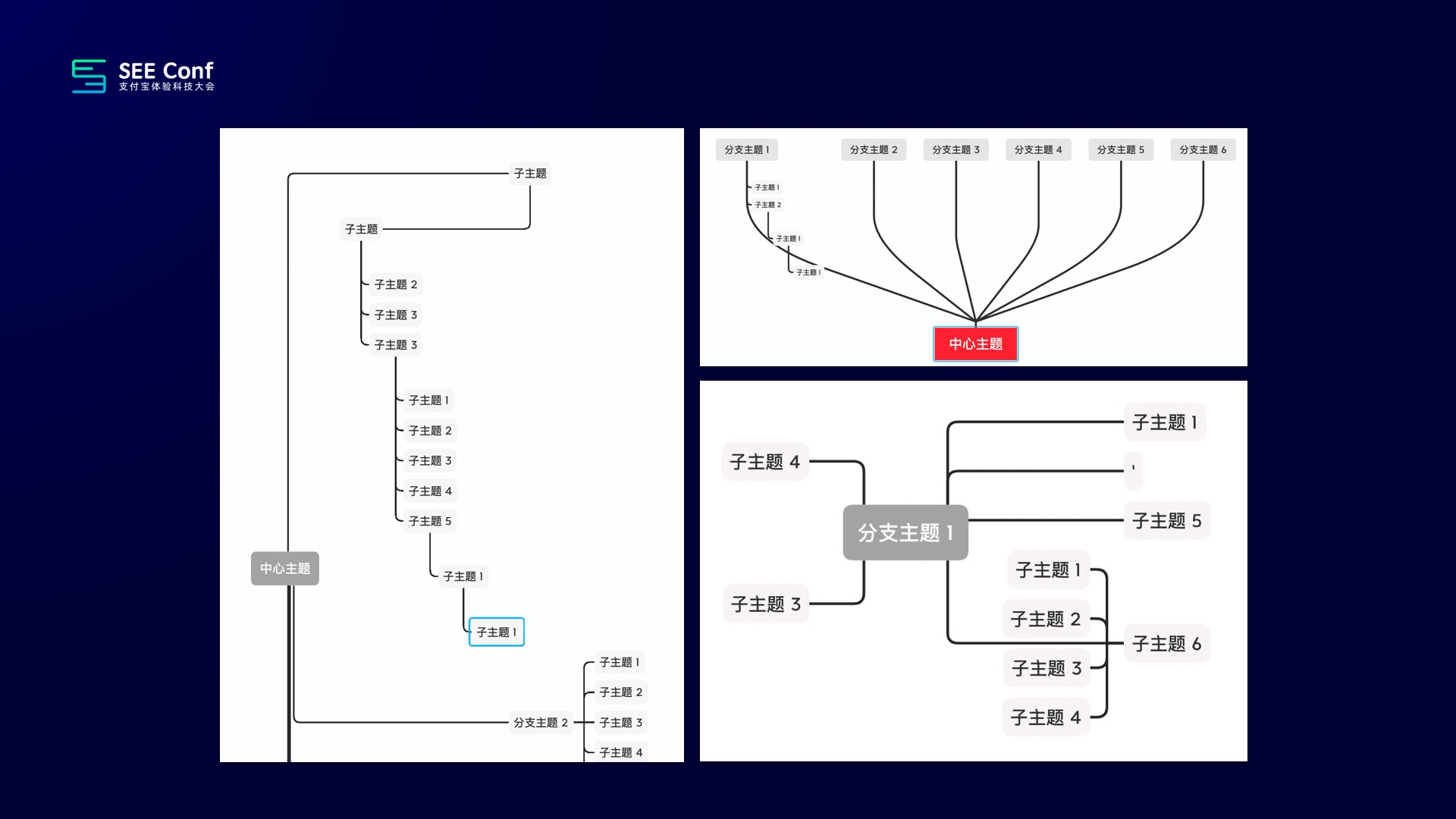
这个方案也是比较大的，所以只能抽中间一个比较精华的部分跟大家分享。

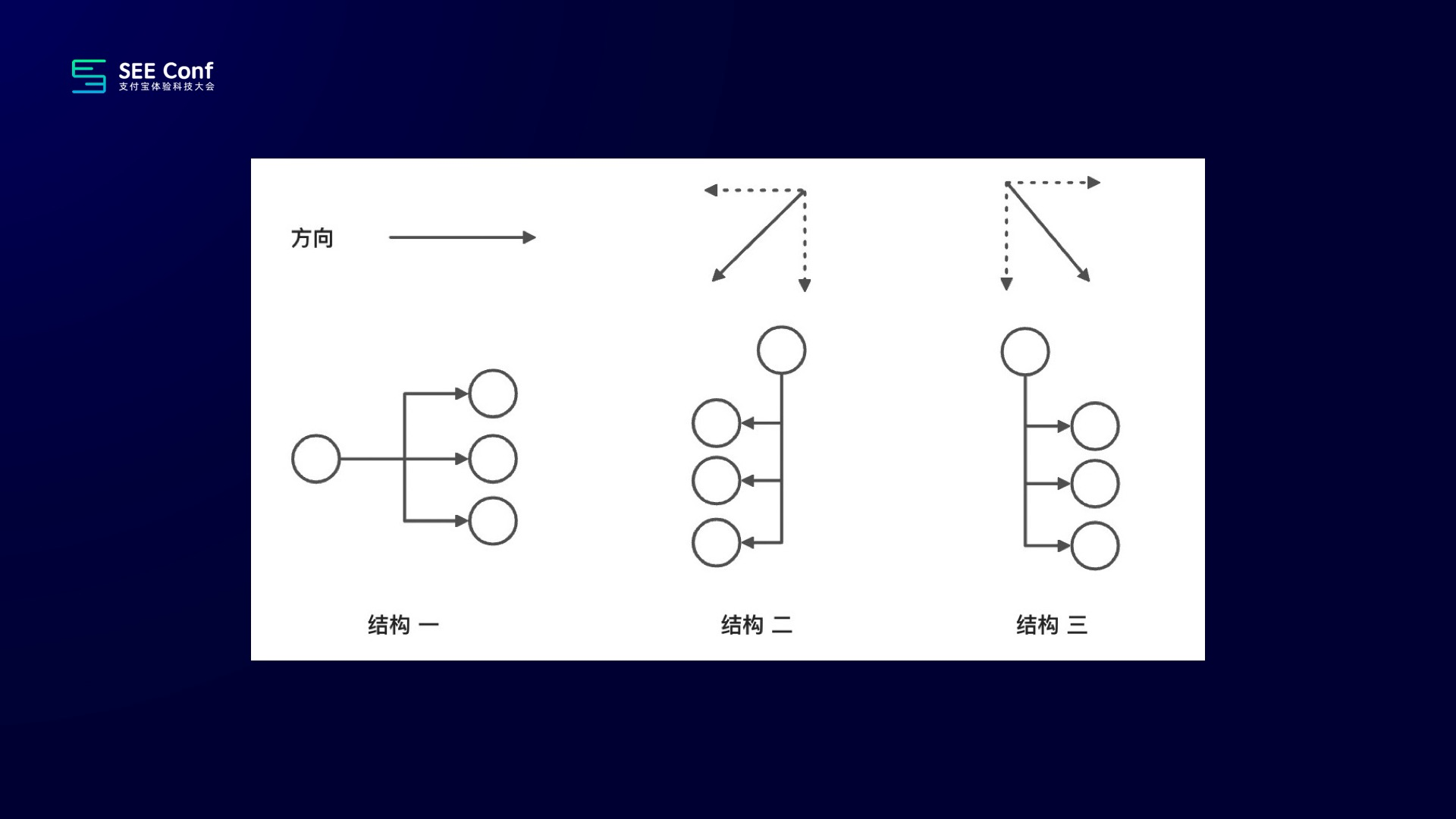
在具体展开前，需要有一个知识储备，这里需要一点点线性代数的知识。大家都是专业人士，我相信这一点问题都没有。我们首先认为每一种结构它都是有方向的。比如说第一个结构，它的方向是向右，第二个结构方向是向左下，第三个结构它的方向是向右下。每一个向量都可以被拆为水平 X 轴，竖直 Y 轴的两个向量。因为线性代数告诉我们，任二维平面内的任何一个向量都能被两个线性无关的向量线性组合去表达。

好，有了这个知识储备以后，我们就可以进一步讨论我们的方案了。首先很明显，不可能所有结构的组合从产品的角度都是合理，所以我们需要找到一条规则去约束结构的组合。经过项目组内同学讨论，很快我们总结出了原则 1.0，如下图所示：

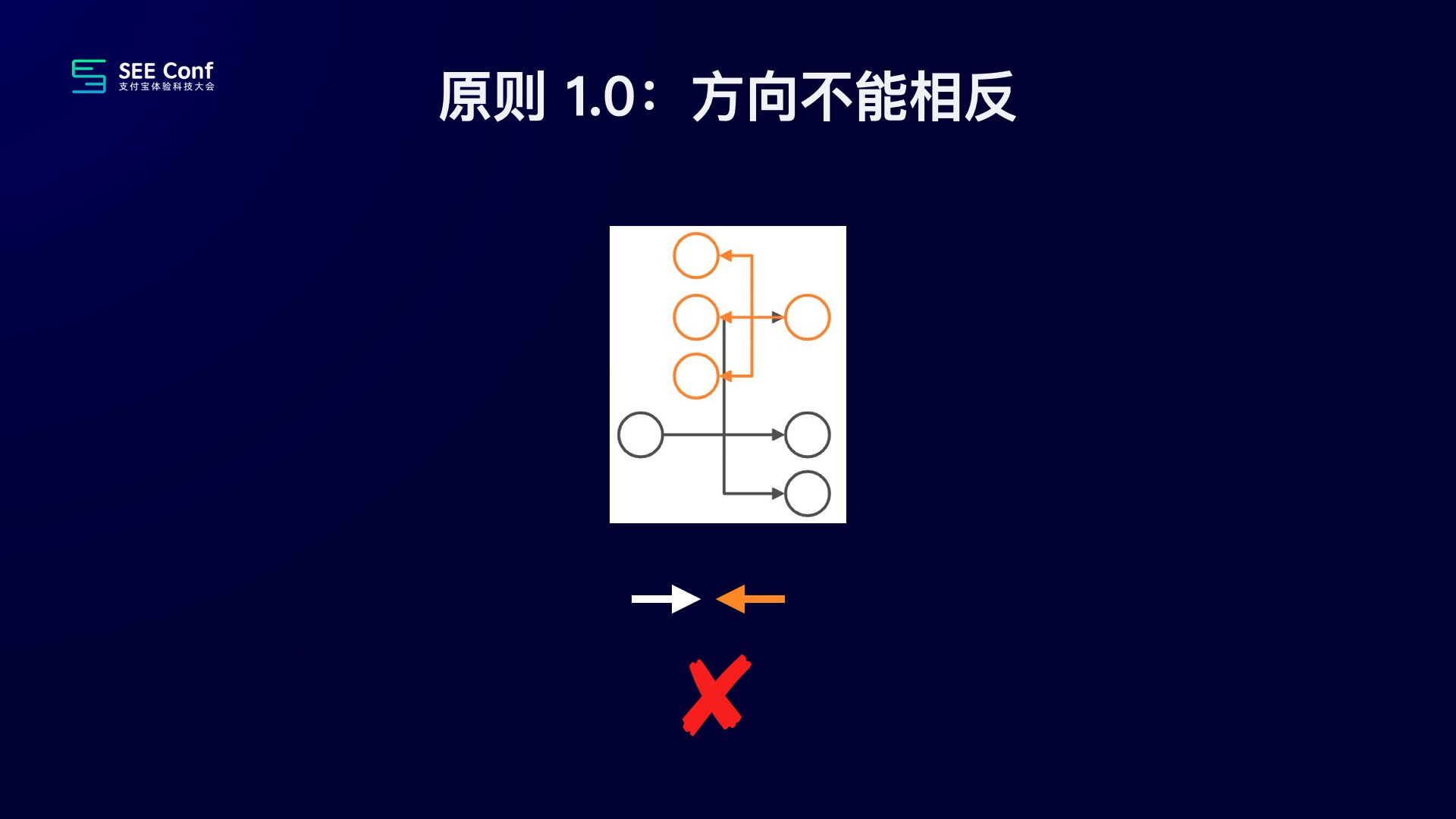
但很快我们也找到了一些反例，于是我们将原来的原则升级为 2.0，如下图所示：

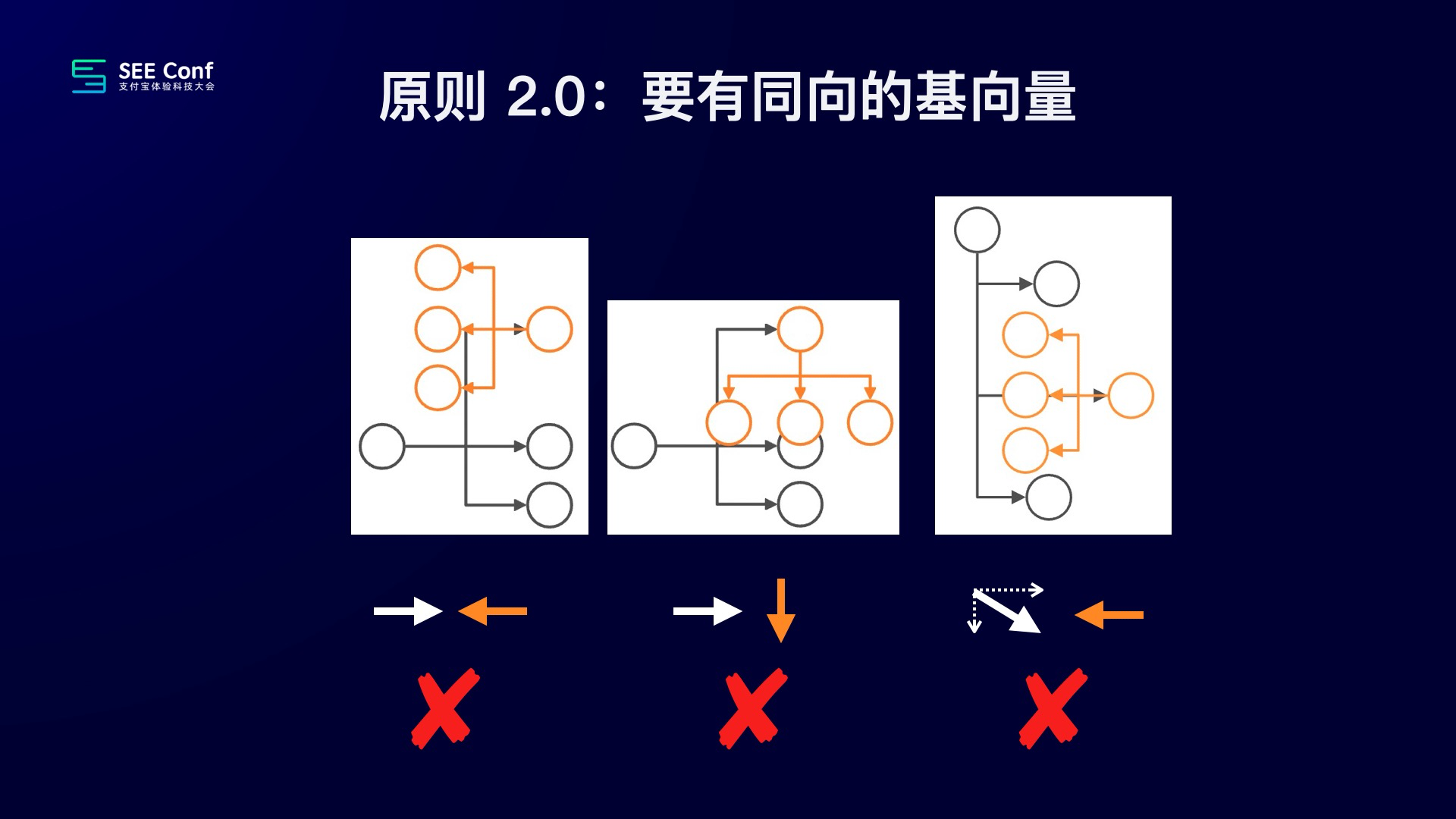
在原则 2.0 下，很长一段时间，我们都觉得运行的很良好，但有一天我们又发现了些，不大满意的组合，于是我们进一步升级了我们的理论，总结出了，原则 3.0：

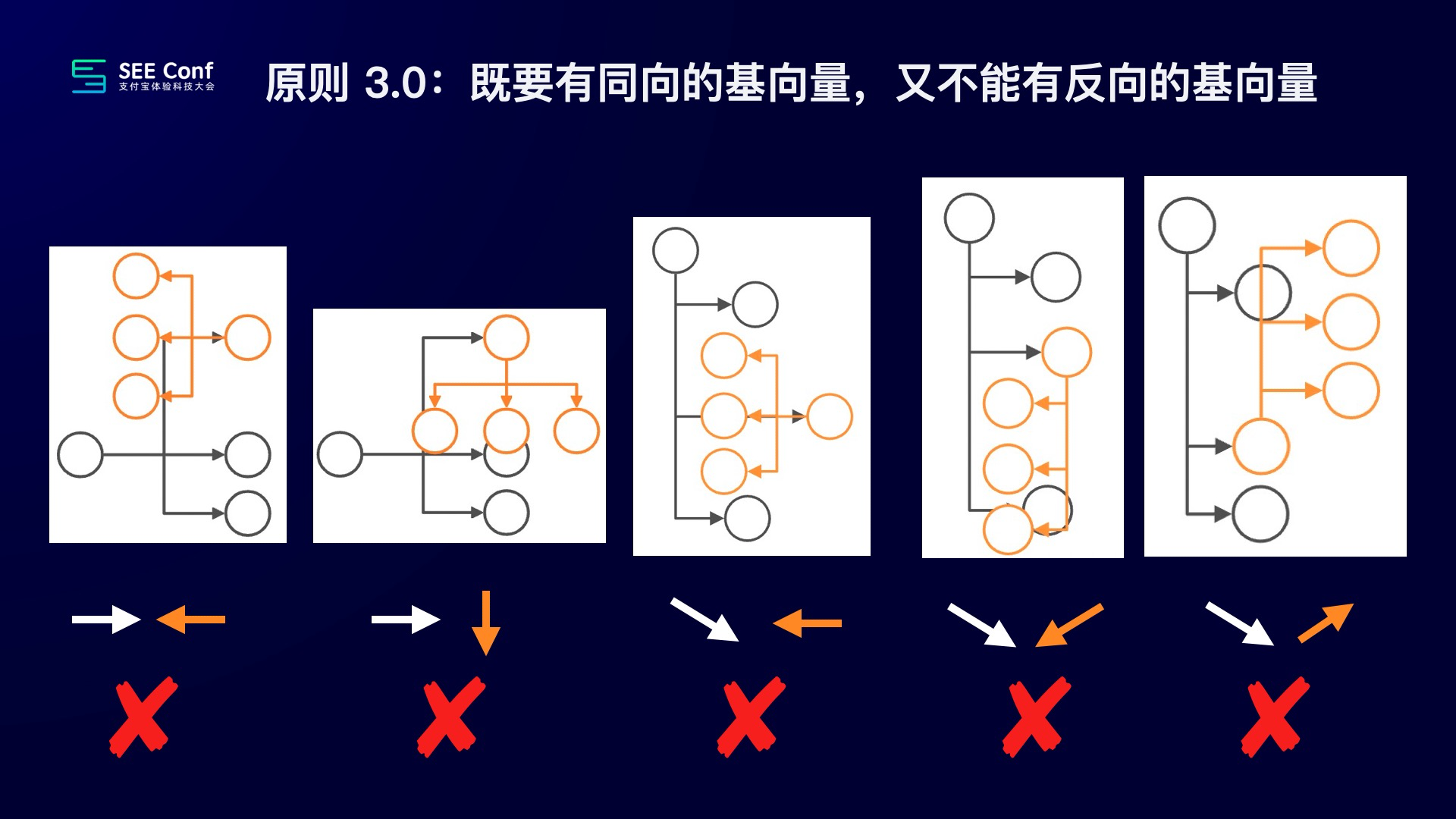
在这个原则的指导下我们得到的结构嵌套组合都比较合理，这里以标准布局和缩进布局的组合举例，以下是我们认为合理、优雅的组合，如下图所示：

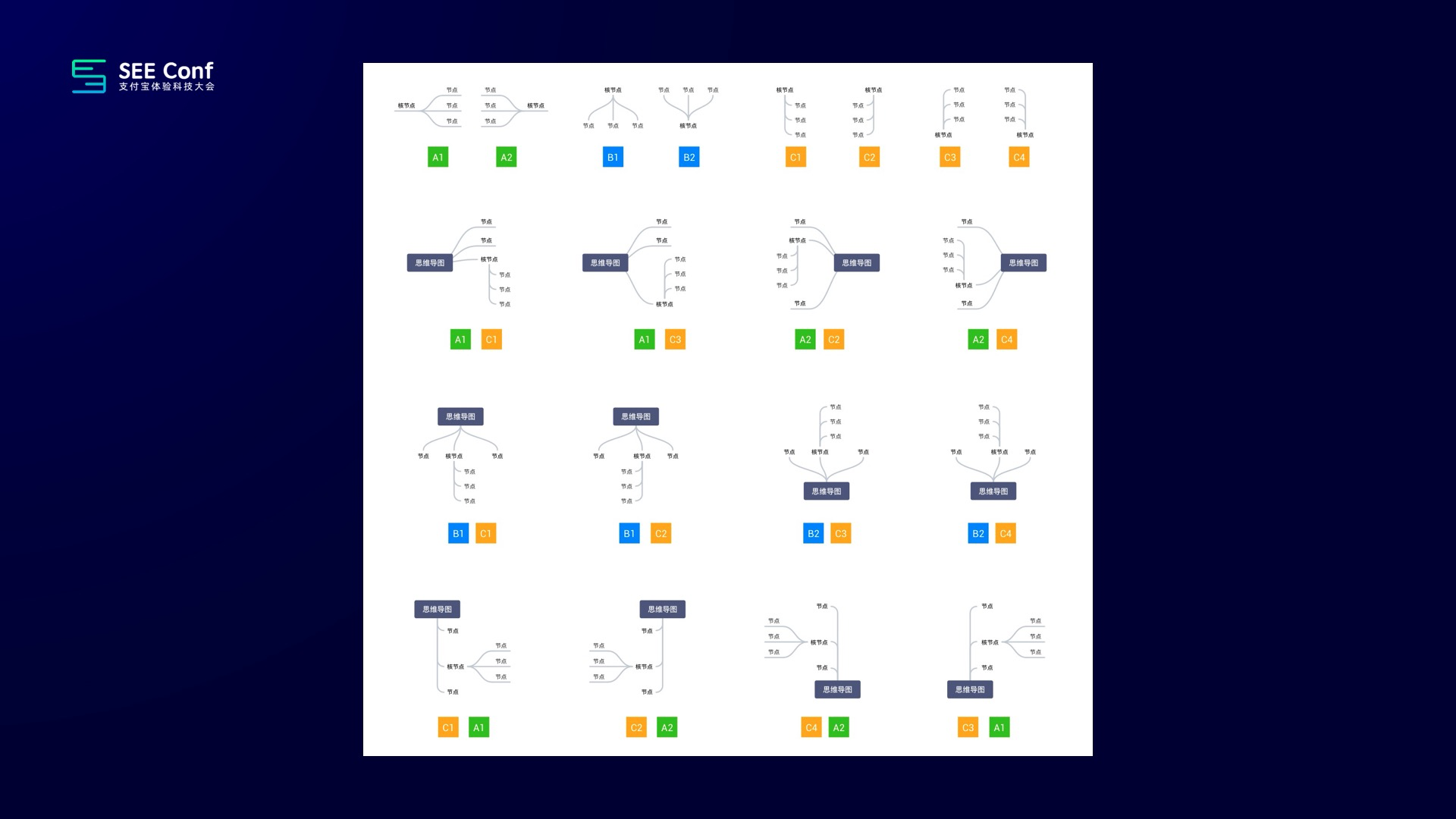
总结

三个故事讲完，今天我的分享也即将结束了，最后，总结一下：

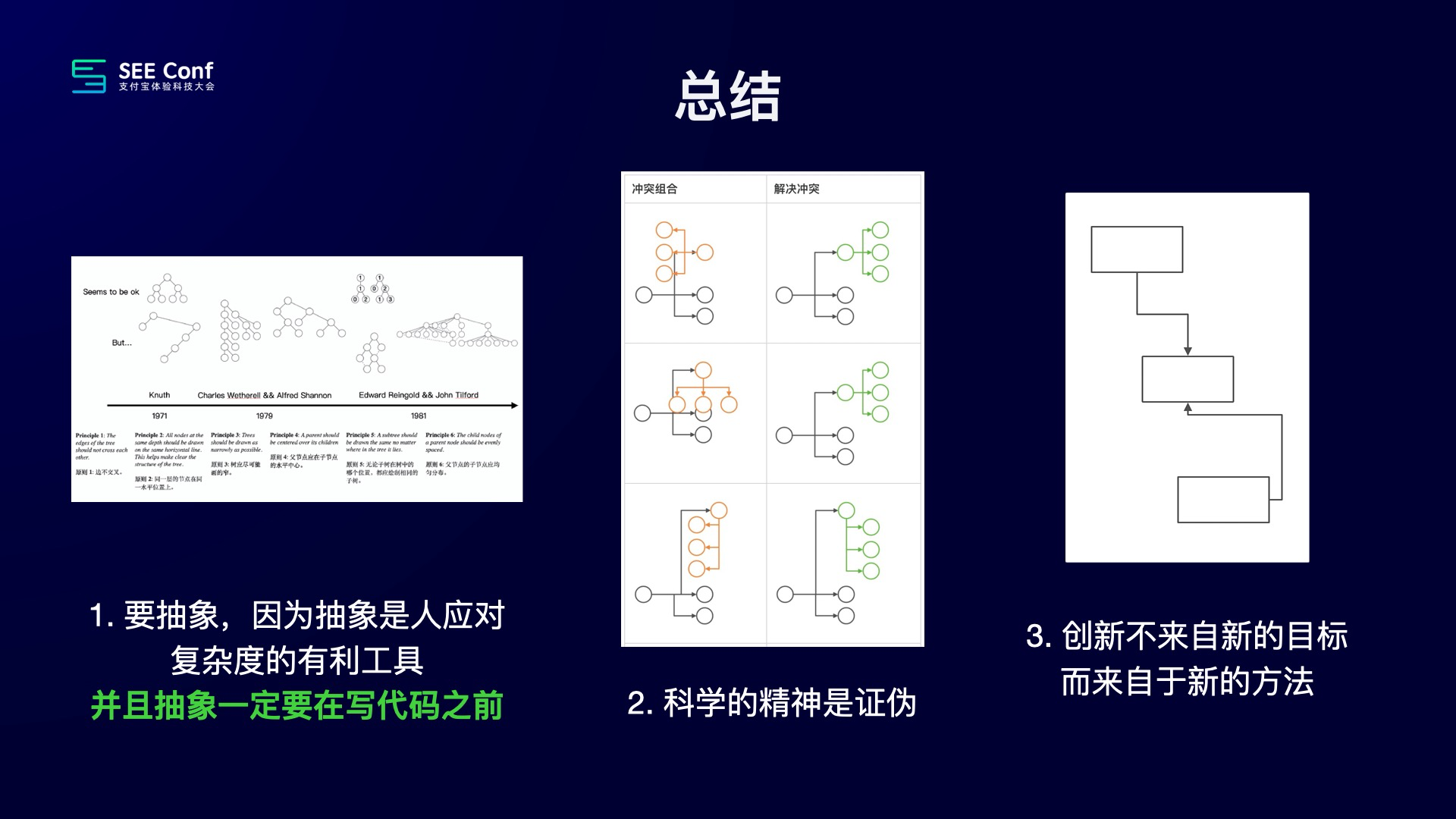
第一个感悟是：我觉得大家在做一些产品功能实现的时候，一定要去抽象。因为其实人是不大擅长去应对复杂度的，然后人的思维，也是很不应适合直接用枚举、用 if else 的方法去解决复杂的任务。所以当我们去解决复杂任务时，一定要去做抽象。但抽象这个事情，在以往工作经验中，往往是到技术研发时才去做，但其实这个是有问题的，因为抽象本身是基于产品理念的，抽象的结果一定是会影响产品功能的。所以这件事情一定要在写代码之前就把它做好。

第二个感悟是：科学的精神是证伪。这句其实大学时期我就常听到过，但我对这句话真正有点理解，应该是做完思维导图子图嵌套这件事情之后。现在回想起来，在做子图嵌套的时候，我们其实就是在做一套小型的科学理论。在这个过程中，其实我们最主要的就是做一件事情：建理论 —— 找反例 —— 改进理论 —— 找反例 —— 改进理论 —— 找反例 —— loop …… 为什么要找反例？为什么要千方百计，想方设法去证明之前自己总结的理论是错的？因为正面的例子，符合理论的例子，对改进理论，毫无用处。

第三个感悟（回到今天的主题【新】上）是：创新的结果，不来自于新的目标，而来自于新的方法。其实创新这个事情，不管是语雀，还是蚂蚁，还是整个国家层面，大家都在提到说要创新。但创新这个结果一定不来自于口号，也不来自于我们的目标，它其实来自于我们想把东西做好的态度，以及日常做事的思维方式和方式方法，只要用对了方法，创新就是一个自然而然的结果。比如，我们在做折线路由的时候，其实大家并没有刻意去追求要和竞品做出点不一样，但因为我们用了一套新的做事方式（就是那六块砖），以至于我们最终做出来的东西有一点点微小而美好的改变。

原文：https://www.yuque.com/seeconf/2022/hvd44m